| SINCE 10 MAR 2008 | ||||||||||||||||||||||||||||
| HOME |
|
|||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
| 本格的な比率の異なる円錐験体の実験に移る前に、進行方向に対して同断面積で、比率の異なる験体のデータを見てみたいと思います。【図-59】はこの実験に用いた験体の数々で、実験は今までと全く同じ方法で行ないます。験体の直径は20mmで各験体の誤差は±0.25mmです。ギリギリに浮力が維持できるように調整してあることは言うまでもありません。 | ||||||||||||||||||||||||||||
 【図-59】 実験に使用した比率1:1.5~1:4.0の各験体
|
||||||||||||||||||||||||||||
| 行なった実験は、①瞬間負荷、②0.5号のオモリを負荷した連続負荷、③水面上10cmからの自由落下の三通りです。共に到達限界深度で結果を表示しました。尚、実験②では、最初に着底した験体を基準に、その時点での他の験体の到達深度を表示しました。 結果から判るとおり、特定な条件下では特に有利な形状が存在していることは確かなようです。重要なのは、流れに対して垂直な面への投影面積、即ち断面積が等しく、表面積、重量、体積が異なるにも拘わらず、特別に優れた動きを示す比率があることです。これは現実のウキに最も適した比率が存在することを示唆しています。 ●結果【図-61】:連続負荷実験では、験体の比率が大きくなればなる程、その体積に対してのオモリ(負荷オモリ)の占める割合は小さくなります。それにも拘わらず比率1:4.0では、今までなだらかな線を描いて低下していた到達深度が、急に1:3.5よりも深くなります。大変興味ある現象と言えます。 また、瞬間負荷と水面上10cmからの落下では、比率1:3.5まではほぼ同じ割合で限界到達深度まで沈降しますが、瞬間負荷では比率1:4.0が急激に後退し、水面上10cmから落下させたものでは、比率1:2.0で限界深度が急に浅くなります。また連続負荷で比率1:4.0が1:3.5を凌駕します。これらは面白い現象です。ただ比率が大きくなるに従いその体積が増大していることを考慮してデータを見る必要はあります。 これらの実験以外に、同体積で比率の異なる実験と、同表面積で比率の異なる実験とを行ないましたが、データを消失しています。面白い結果でしたのでまったく残念です。 |
||||||||||||||||||||||||||||
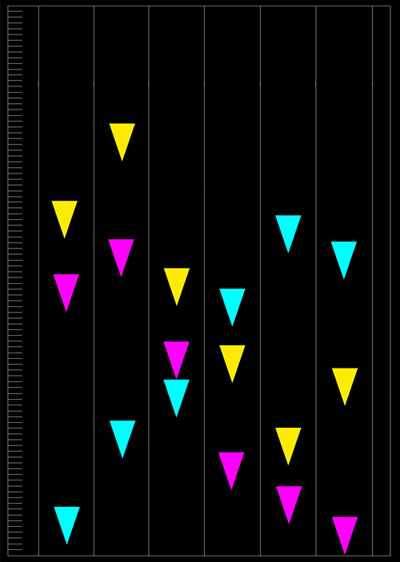 【図-61】 棒状験体の到達限界深度 水温12℃±1℃ ▼黄色:瞬間負荷 ▼青:0.5号の連続負荷 ▼桃:自由落下 |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
いよいよ核心の円錐験体での本格的比較実験に移ります。ここでは前記の核実験から得られたデータを基に、比率の異なる円錐験体(ドングリ型とシズク型)の運動能力の観察を行ないます。 製作した験体は、直径が29mmで流れに対して直角の面への投影面積が等しい、比率が1:1.5・1:2.0・1:2.5・1:3.0・1:3.5・1:4.0・1:4.5・1:5.0・1:5.5の9種類を2組計18体と、同体積で比率の異なるもの、同表面積で比率の異なるものとの、総計54体です。それぞれの験体の誤差は±0.25mm以内で、浮力調整も慎重に行なっています。 残念なことに、直径29mmの験体以外のデータが消失しています。故にこれらの実験データは割愛しますが、理想の形状を求める上で何ら障害にはなりません。ただ検証データが減るだけのことで、大きな問題ではありません。(オイオイ!) また、事前の試行で当初用意した験体の内、運動能力が極端に見劣りする、比率1:1.5・1:2.0・1:2.5の3体を外し、6体ずつの計12体にて行ないました。 実験は4種類で、実験①は0.5号のオモリを負荷し単一時間内の沈降深度を観察し、実験②は同じく1号を負荷し、実験③は負荷オモリ無しで験体頂点に打撃を与える瞬間負荷で到達限界深度と浮上所要時間を観察します。実験④は、水面上からの自由落下で、沈降深度と浮上所要時間を観察します。この④はシズク型とドングリ型とを別々に行いました。これはの能力差が大きすぎ比較の意味が無いからです。 実験はそれぞれ10回行ない、計測は巻尺と目測ですので完璧ではありませんが、順位に関しては図の通りです。尚、この一連の実験では水温の管理は一切行なっていません。 ●実験①の結果【図-62】:実験は左から右へそれぞれ比率 1:3.0・1:3.5・1:4.0・1:4.5・1:5.0・1:5.5 の6体の験体で行ないます。緑がドングリ型、橙がシズク型です。この実験では、6験体の中で最初に着底した験体を基準に、その時点での他の験体の沈降深度を観察しました。 【図-61】で「…特別に優れた動きを示す比率があることです。これは現実のウキに最も適した比率が存在することを示唆して…」と書きましたが、正に比率1:4.5がこれに該当します。【図-62】でこのダントツの運動性能が証明されたと考えても間違いではないと思います。単一時間内での沈降到達深度は、ドングリ型の約2倍に達しています。 ●実験②の結果【図-63】:これも①と同じ験体を使用します。6験体の中で最初に着底した験体を基準に、その時点での他の験体の沈降深度を観察しましたが、シズク型では比率1:4.0を除き、全てがドングリ型が着底しない内に着底してしまいました。ドングリ型では比率1:4.5が成績を落とし、1:3.0を除き綺麗な斜め一列に並びました。現実のウキとしては余り意味のある実験とは思えませんが、結果としては面白いものがあります。 ●実験③の結果【図-64】:使用する験体は前の①②と同じものですが、追加の負荷オモリを使用せず、打撃装置をしようしてエネルギーを与えました。ここでも比率1:4.5が目を見張る速度で沈降し着底します。浮上の所要時間は比率1:5.5が浮上した時点での計測で、特に比率1:4.0~1:5.5の浮上能力が優れています。 比率1:4.5は着底しまうので計測できませんが、他の験体より深く沈降するのでダントツな浮上能力とはいかないとは思いますが、一連の実験から得られたデータから予測すると、いち早く浮上運動に移行するので、悪い結果は出ないと思われます。機会があれば是非確認したい点です。 |
||||||||||||||||||||||||||||
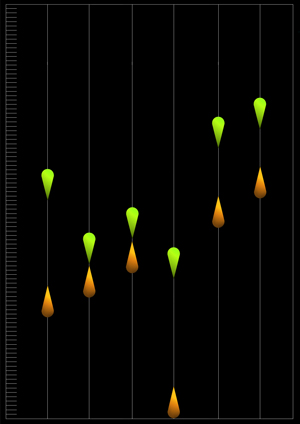 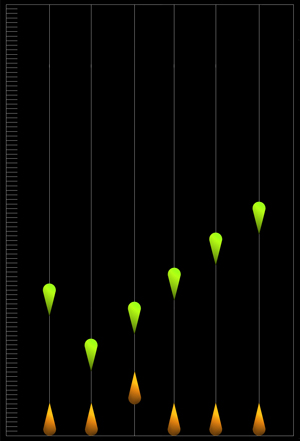 【図-62】 0.5号負荷時の到達限界深度 【図-63】 1号負荷時の到達限界深度 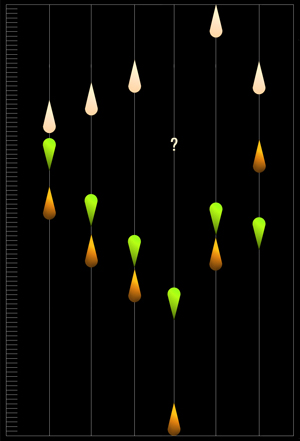 【図-64】 瞬間負荷での単一時間内の沈降深度薄い色は浮上所要時間を示します |
||||||||||||||||||||||||||||
| ●実験④-1の結果【図-65】:予想どおりのシズク型験体の結果です。瞬間負荷とほぼ同じ結果と言えます。水面上からの自由落下実験や瞬間負荷実験は、比率の異なる験体のエネルギー保存能力を探るのには、適切な手段であった言えます。【図-65】は最初に着底する比率1:4.5の験体が基準になった単一時間内の沈降到達深度です。 浮上順位に関しては、最初に着底した比率1:4.5は除外してあります。 ●実験④-2の結果【図-66】:ドングリ型は落下高度が沈降深度の伸びに大きな影響は与えず、高度100mm、10mmとも着底しません。比率1:3.0に至っては高度300mmからの落下でも着底しませんでした。 |
||||||||||||||||||||||||||||
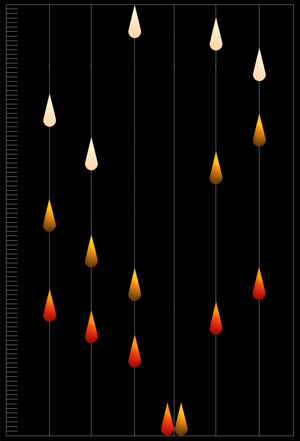 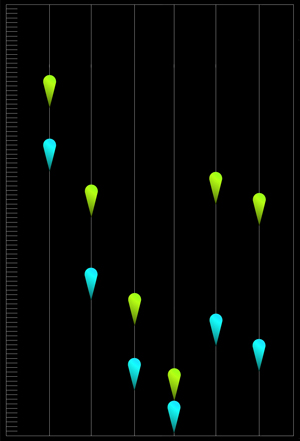 【図-65】 赤が水面上100mm 橙が10mmからの自由落下 クリームが浮上能力 【図-66】 青が100mm 緑が10mmからの自由落下 |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
| 球体に始まり、阿波ウキのドングリ型とシズク型、そして比率の異なる棒状験体や円錐験体と、実験を通して数々の貴重なデータが得られました。この中には実験してみなければ絶対に判らないことが多く、「目から鱗」のようなものも数多くあります。 円錐験体の総括に移る前に少し棒状験体に触れておきたいと思います。この棒状験体は実験に移る前から高い粘性抵抗を予想でき、瞬間負荷実験では一番重い鉄製のハンマーを使っています。実験結果を示した図を見て円錐験体と互角の能力を持つと誤解しないで下さい。 下の【図-67】の左側が実際に使用した験体で、円柱の上下に半球をくっ付けた形状をしています。頭部と下部(どちらが頭部でどちらが下部か?)が半球である必要はなかったのですが、球体は同体積で最小の表面積を持ち、同表面積では最小の体積を持つ三次元物体で、完璧な曲線により構成され、検証する対象である円柱に対して占める割合(体積比でも表面積比でも)が少なく、且つ接続面に鋭角な面を形作ることが無く、また棒状験体の特性に与える影響が最小だろうと考えたからです。 ここには紹介しませんでしたが、【図-67】の右側のような頭部がなめらかな線で収束する験体での実験も行ないました。データは消失しましたが、左側の験体と比較すると、極端に運動能力が高まります。これは流れの方向(後部)に、境界層の剥離を極端に生じさせる、急激な収束形状または鋭角面を持たないからと言えます。逆に突入方向の形状をなめらかな形状に加工した験体ではさほどの改善は見られませんでした。 ここから一つの答えが導き出されます。それは「流体中を運動するウキは、その突入部の形状ではなく、後部の形状により運動能力が左右され、エネルギー保存に寄与したり損失を与えたりする」と言うことです。ウキに関して言えることは、半球は突入部の形状としては最適と言えます。当然、なめらかな表面と一切の鋭角部分を持たないことがその大前提となります。 |
||||||||||||||||||||||||||||
| 理想的なウキの形状は「円筒状部分を極力有さず、突入部は体積、表面積、共に最小で滑らかな曲線で構成され、且つ後部は可能な限り小さく、境界層の剥離を早期に招く鋭角な面を持たず、円滑に収束する形状」だと言えます。ここまで来れば凡その姿は見えてくる筈です。 | ||||||||||||||||||||||||||||
  【図-67】 半球と滑らかに収束する形状を持つ棒状験体 【図-68】 他の形状を有する験体 |
||||||||||||||||||||||||||||
| 実際にはここに記した以外にも【図-68】のようなイロイロな形状の験体を製作しましたが、左の験体以外に感心できる結果を出せたものはありません。共に最大幅29mmの験体で、誤差は±0.25mmです。結局一連の実験の為に製作した験体は合計で200体を越え、製作と一連の実験に1年間を費やしました。 多くの験体の中で唯一シズク型験体に近い結果が得られたのが【図-70】の流線型の験体です。この流線型の比率1:3.5~1:4.0は高速流体中では理想的な形状と言われています。また流線型の験体は連続負荷実験ではシズク型験体と互角な結果を示しますが、極めて小さい瞬間負荷では比率1:4.5のシズク型より劣るようです。 いずれにしても全てのデータがシズク型の優越性を証明しています。特に比率1:4.5の験体は突出した結果を見せ付けました。これは粘性抵抗の影響を受け難い形状であることを示唆していると共に、この形状のウキは運動性能が非常に高いと言っても差し支えないと思います。 粘性抵抗が高いドングリ型であっても、比率1:4.5の示す運動能力が比較的高いと言うのも面白い結果です。さらにドングリ型は浮上能力では、沈降時のシズク型同様に高い運動性能を示しますが、自由落下実験で判るとおり、その限界深度までに緩慢な動作で沈降する為に、浮上行動に移行するまでに多くの時間を費やし、結局は浮上までの所要時間はシズク型に劣る結果となりました。これは「立ち上がり」の遅いウキを連想させます。【図-69】はドングリ型単独の浮上実験で比率1:5.5の験体頭部が水面上に到達した時点での他の験体の位置を示します。この実験で使用した験体は直径29mmで誤差±0.25mmです。 |
||||||||||||||||||||||||||||
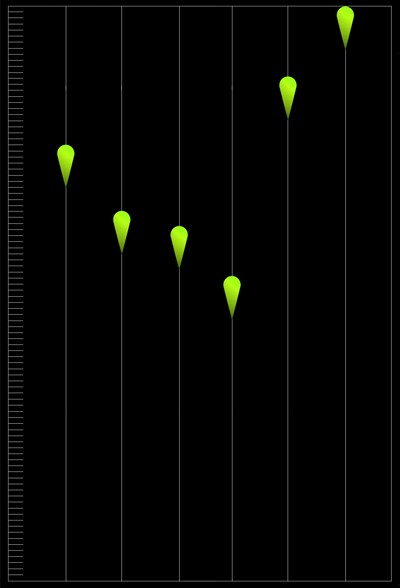 【図-69】 ドングリ型験体の離底実験  【図-70】 高速流体中での理想的形状 |
||||||||||||||||||||||||||||
 Traditional Japanese colors |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
