| SINCE 10 MAR 2008 | ||||||||||||||||||||||||||||||||
| HOME |
|
|||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||
| 株式会社計算流体力学研究所 「境界層の剥離と後部渦流」 とても面白いので一度訪れてみて下さい |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
皆さんは市販されているウキが、どの様な過程を経て、世に送り出されているとお考えですか。当然、幾多の水槽実験と試行錯誤を経て開発、製造されているとお考えでしょう。確かにそのようなメーカーも存在するでしょうが、多くのメーカーは昔のままの作業を続けているに過ぎません。 市販されている製品を見る限り、開発過程に於いて流体力学(水力学)的考察を試みているメーカーは、本当に存在するのか、甚だ疑問だと言わざるを得ません。形状の決定に際しては、水槽を用いて抵抗値を計測する程度と思われます。 水槽実験では、各種形状の験体(ウキの模型)を用意し、一定流速中での抵抗値を計測しますが、浮力を上回るオモリを負荷し、沈降試験を行なうのが一般的です。つまり連続負荷状態の運動能力(この場合は抵抗値)を観察し、優秀な成績を収めた験体が目的にあった形状とされ、製品のモデルとして採用されることになります。メーカーがこのような過程を必要とするのは、流体力学が実験科学として成り立っている以上当然の手続と言えます。 しかし、この種の実験が抱える問題は、実際のウキの動きが全く反映されていないことにあります。ウキは波浪中を浮遊し、多種多様な予測できない動きを見せます。その運動が一様であると言うことは、まず考えられません。ましてや、単純な連続負荷をかける沈降実験などでは、定常運動中での安定性の観察以外、何の意味も持ち得ません。ウキの観察は潜水艦や魚雷の抵抗値の計測とは異なります。連続負荷の沈降実験は、全く的外れな実験と言わざるを得ません。このことも後に詳しく述べます。 |
||||||||||||||||||||||||||||||||
  レオナルド・ダビンチ Leonardo da Vinnci 1452-1519 |
||||||||||||||||||||||||||||||||
| イタリアに生まれた天才。現在の科学水準に照らしても遜色の無い研究と成果を残し後の科学発展に多大な影響を与えた。流体力学の分野でも目を見張る業績を残している。 右上が有名な「ミロのビーナス」 下が彼が描いた境界層の剥離と渦流 | ||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||
| 近代に於ける流体力学は、より多くの物を如何に効率的に輸送するかという、産業界の商業的要請に応えて生まれた学問です。つまり過去に於いて流体力学(現在ではサポート範囲が多岐にわたり欠かせない学問となっています)は、主に如何に多くの流体を、パイプを介し、短時間の内に、より遠くまで輸送できるかを研究する学問でした。 1883年、イギリスの物理学者・技術者であったオズボーン・レイノルズ(下の写真)は、パイプの中を流れる流体が規則正しい一定の層をなす「層流」と不規則な渦をともなう「乱流」とで構成されていることに気づき、有名なレイノルズ数を発見します。 |
||||||||||||||||||||||||||||||||
 オズボーン・レイノルズ Osborne Reynolds(1842~1912) |
||||||||||||||||||||||||||||||||
| このレイノルズが発見した無次元数では、「流体中の物体の抗力係数 Re は、その物体の密度、粘性係数、速度および形状や大きさに関係している」と定義されています。ウキのような小さい物体に他の物体の計測で得られた結果をそのまま適用することに問題があることを予見させます。 流体の挙動を研究することは、多くのパイプラインが、複雑に交差するような化学プラントや、流れの影響をもろに受ける橋げたの設計等では、無くてはならない重要な学問です。 しかし過去も現在も、流体力学が高速の流れがその主な目的の学問であるということには変わりはなく、このポイントを外した実験は、本来の目的から大きく逸れる結果を招きます。 流体力学は、その発生当初からウキのような低速移動体を対象にはしていません。魚が餌を吸い込む際の初期動作がウキに及ぼす影響は差ほど大きくはなく、その速度は恐らく5km/hを超えることはないと考えられます。これは秒速換算では約1.4mに相当します。1秒間に1.4mも沈降するウキなど誰が想像できるでしょうか。 つまり、低速で僅かな距離を移動(アワセに必要な沈降距離は、せいぜい30cm程度)する物体が「ウキ」なのです。針掛かりしてしまえば、それこそ無用の長物と言えます。 しかし、魚が摂餌するまでにウキには様々な条件が要求されます。不確定要素の塊のようなフィールドで使用されるウキに、浮力を大幅に上回るオモリを負荷したような、単純な沈降実験など「愚の骨頂」以外の何物でもありません。 ウキが連続的に定常運動することなど考えられません。若しあるとすれば、それは唯一針掛かりした魚が突っ走った時だけでしょう。向こうアワセでの針掛かりでは、ウキの感度など何の意味も持ちません。如何に意味の無い実験を土台にしてウキが語られているかの査証です。 |
||||||||||||||||||||||||||||||||

|
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
ウキの形状研究は、海中を高速で移動する潜水艦のそれとは異なります。人によって目的とする要件の比重が異なるますが、私が特に重要視しているのが「前触れアタリ」です。虫餌の摂餌に際しては、一度吸い込んでから、軽く吐き出し、次に本格的に摂餌に入ります。 スズキなどが小魚を捕らえる際は、一度体当たりをしてから反転して呑み込むと言われていますが、これは魚の目が両側に位置し直前の餌が死角になり見えないためとも言われています。 私がウキに求める条件は、この餌を一度吸い込んでから、再び軽く吐き出す一連の行為を、如何に的確に表現できるかです。 つまり、この最初の餌を吸い込んだ瞬間に、鋭敏に反応する「即応性」と、「前触れアタリ」だと視認させる豊かな「表現力」です。 魚は餌を吸い込む際に異常を感じると、警戒心を高め、本格的な摂餌行動には至りません。故に、この一瞬が非常に重要な要素になります。何故ハリスがしなやかで細くなければならないかの理由がここにあります。このことも読み進めるとうちに自然と理解することができ、「魚は目が良いからとハリスを細くする」言う理屈は、根拠がまるで無いとお解り頂ける筈です。ハリスを細くするのはまるで異なる理由からなのです。 即応性の高いウキは、最初に餌を吸い込む僅かなエネルギーを、ミチ糸を介し確実に表現できます。また即応性が高く敏速に反応するには、運動エネルギーの損失を最小限に抑え、沈降への原動力とする慣性能力を求められます。 最初の瞬間的な負荷に対する運動エネルギーの保存能力が優れているとウキは、エネルギーの損失が少なく、沈降動作を一定時間保持し続けることが可能で、「前触れアタリ」に即応し、確実にこれを表現でき、本格的な引き込みに対して充分な備えが可能になります。 ウキが水中深く引き込まれるた時は、よほどマヌケでない限り、誰でもしっかりとアワセられる筈です。大切なのは本格的な引き込みが始まる前の「前触れアタリ」です。 この前触れアタリを豊かに表現できるウキは、それが本格的な引き込みの前触れなのか、小物が餌を突っついているのか、水中の様子が手に取るように判ります。 「前触れアタリ」でお判りいただけるかと思いますが、データ収集は瞬間負荷への即応性と、その慣性運動エネルギーの保存性能の高さに重点を置いています。ウキの運動は全てが過渡的に推移し、定常的なものは何もありません。 永きにわたる専門家の研究により蓄積された膨大な流体力学の成果は、ウキの理想的形状を求める上で重要な意味を持ちます。ただ一般的には流体力学(水力学)は、流体中を定常運動する物体をその前提条件としていますので、不安定要素が複雑に絡まるウキの世界に、そのまま当てはめる訳には行きません。 然しながらその意味と目的とを理解し、正しい方法で実験を重ねることが出来れば、必ずやそこから大きな成果を得られる筈です。 |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
ウキの運動特性を解明するには実験を重ねることが第一で、理論付けはその後になります。つまり実験科学である流体力学の手法そのものと言えます。 ウキは波浪中で様々な複雑な動きを見せ、どうこれを再現しつつ実験を重ねるかが重要な要素となります。特別な実験設備など持たない者にとってこれは大変大きな問題と言えます。 理想から言えば、実験設備として、直径300mm×1.5m程の水をはれる透明なアクリルパイプがあれば良いのですが、そうもいかず、結局は600mm程度の水深を実現できる家庭の風呂桶に落ち着くことになりました。しかし、考え方によれば600mmあれば充分で、600mmもウキが沈降するような時は、完全に針掛かりしている時で、これは目的とする「前触れアタリ」や「表現能力」の段階を過ぎているからです。前述の通り針掛かりしてしまえばウキの形状など何の意味も持ちません。後は釣り人の技術の問題だけです。 実験結果に関して書く前に、流体力学(水力学)の基礎中の基礎である、幾つかの項目を理解して頂く必要があります。そして次に、何故ウキの研究をするようになったかのキッカケを説明したいと思います。下の表【表-1】は各種液体の圧縮率です。 |
||||||||||||||||||||||||||||||||
【図-1】各種液体の圧縮率 |
||||||||||||||||||||||||||||||||
| 因みに真水の圧縮率も大変低く、20℃の10mm×10mm×10mm(1ccのことです)の水の上に1kgの重石を乗せた場合、約0.45μm圧縮されます。μは長さの単位で、1mmの100分の1を表します。つまり10000分の45mm圧縮されると言うことです。空気は圧力を加えて簡単に縮めることが可能です。その良い例が圧縮空気を作り出すコンプレッサーです。これに反し水を含む液体は、殆ど圧縮されないことが【図-1】からも容易に理解できます。 流体には気体と液体の2体(厳密には固体も含まれる)があり、このうちウキの運動に関与するのは前者では投入時と水面に吹く風ぐらいで、残りは全て後者の液体となります。 このウキの運動に大きな影響を及ぼす液体には、重要な二つの性質があります。一つは【表-1】から判る低圧縮性と、高粘性です。粘性とはいわゆる「ネバリ」のことです。この粘性は真水で空気の凡そ55倍あります。 水の圧縮率の低さはプールでも飛び込みを思い浮かべれば明らかです。飛び込みに失敗すると恐ろしく痛い思いをします。多くの人が子供の時に一度はこの「腹打ち」の洗礼を受けた経験がある筈です。水の圧縮率が高ければ痛い「腹打ち」を避けられたのでしょうが、今度は高圧縮率のお陰でプールの底に顔面を打ちつける結果となります。高圧縮と言うことはプールに空気だけが入っているようなものです。飛び込みは「無謀」そのものとなります。 ウキはこの低圧縮で高粘度の双方の影響から逃れることは出来ず、常にこの性質の支配下で高い運動性能を追求しなければなりません。この物体が受ける影響を、流体の運動に関係すると言うことで「動粘度」と呼び、一般に下の式で表されます。動粘度は粘性の程度μを流体の密度ρで割った値γで表します。 |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
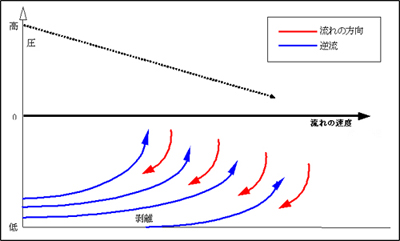
【図-2】境界層の剥離と後部渦流発生のメカニズム |
||||||||||||||||||||||||||||||||
|
粘性のある液体(実在する液体には全て粘性が有ります)が固体の表面に沿って流れる場合、その表面に密接した部分の液体は、固体に密着し、その速度はゼロになります。この流れない表面にへばり付いた極めて薄い層を、流体力学では「境界層」と呼んでいます。 この境界層は、固体表面から離れるに伴い徐々にその速度を増します。そして速度の増加に従い、固体から離れる流れとは逆方向の、高速の流れが入り込み「乱流」を発生させます。この乱流により流体中の固体は、固体表面と流体との間に、流体の粘性に基づく「せん断応力」と言う粘性抵抗が働きます。つまり互いの流れに逆方向の流れのズレが生じる訳です。この現象を「流体摩擦」と呼び、境界層内の流れの状態と固体表面の状態に因って異なります。 一般にはこの流体の粘性に基づく「せん断応力=流体摩擦(粘性係数)」は流体の温度の上昇に伴い減少する傾向があります。ヨットマンが「冬の風は重い」と表現する理由がここにあります。 粘性を持った流体が固体表面に沿って流れ、その速度が下流に向かって増加する場合、その圧力は固体表面に於いて下流に向かって下降します。下流に向かって速度が低下すると、その圧力は固体表面に於いて下流に向かって増加します。このことはウキの形状を求める上で非常に重要な意味を持ってきます。 この流れがある時点で固体表面から離れ、外層から逆方向の流れが押し寄せ、乱流を発生させる現象を「境界層の剥離」呼びます。上の動画はこの境界層の剥離とその後に発生する後部渦流の状態を現しています。【図-2】はそのメカニズムを解りやすく図表化したものです。 ゴルフ・ボールは表面にディンプルがあることにより、故意にボール表面に早い段階で小さな乱流を作り出し、境界層の剥離を極力後ろ方向にずらすようになっています。このことによりディンプル有りのボールは、無しのボールと比較しより遠くへ飛ばすことができるようになりました。 ウキの世界でもこのディンプルを施したものが有りますが全く理解に苦しみます。空気は水の55分の1の粘性です。またゴルフボールはインパクト時で秒速50m以上の速度があり、且つ高速で回転しながら飛翔する物体です。ウキは粘性の高い流体中を低速で運動します。ディンプルを施してもいたずらに表面積を増やし、表面摩擦が増大するだけで何の意味もありません。 |
||||||||||||||||||||||||||||||||
 ゴルフボールのディンプル |
||||||||||||||||||||||||||||||||
| 【図-2】に示される通り、固体表面の流れはある地点で固体表面から離れ、外層から逆方向の高速な流れが押し寄せ、乱流が発生し、それが後部渦流を引き起こします。この渦流の発生部分では圧力が低下し、進行方向とは逆方向の吸寄せる力が働きます。流体中を移動する物体は、渦流発生に伴い、抵抗が増大し、大幅にエネルギーの損失を招くことになります。 一般に流体中で運動する物体の抵抗は、大部分がこの後部に発生する渦流に起因するものです。ウキも当然この影響を受けます。如何にこの渦流の影響を回避できるかが、ウキの優劣を決定する大きな因子となります。これは形状追求に、一つの方向を示している重要な答えとも言えます。つまり、ウキの運動エネルギーの損失を最小限に留め、より抵抗の少ない形状を模索するには、その後部形状により多くの時間を割くべきとの示唆です。 【図-3】は流体中を運動する物体の受ける抵抗値Dを表わした数式です。CDは定数、Aは一様な流れの方向とその流れに垂直な面への投影面積、Uは一様な流れ、μは流体の粘性を表わします。 ウキは流体中を低速で運動(沈降・移動)する小さい物体ですので、流体力学上の計算値をさほど気にする必要はありませんが、どのように抵抗値は求められるのかを知ることは、これからの実験を行なう上で「知っていて損は無い」筈です。 |
||||||||||||||||||||||||||||||||
【図-3】流体中の物体が受ける抵抗値D |
||||||||||||||||||||||||||||||||
 Traditional Japanese colors |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
