| SINCE 10 MAR 2008 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| HOME |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
  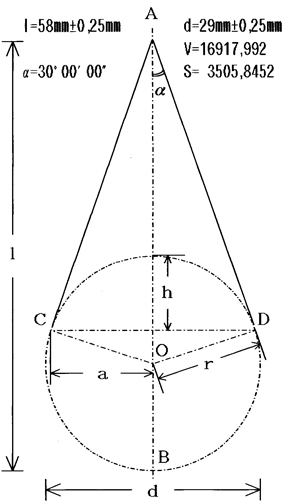 【図-43】 ドングリ型円錐ウキ 【図-44】 シズク型円錐ウキ 【図-45】 使用した験体の実寸 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 験体の製作法は、既に球体の験体製作のところで書きましたが、阿波ウキのドングリ型【図-43】とシズク型【図-44】の験体に関しては、球体と異なり単純な形状ではなく、緻密に調整しなければならない部分が数多いので、重複する部分のありますが詳しく書いておきたいと思います。 使用する験体は実際の阿波ウキとは異なり、浮力調整や各部の微調整の精度を高め、且つ体積と表面積を極力抑える為に、贅肉をそぎ落とし、デフォルメを施しました。 製作した験体は比重0.17の高級バルサ材を使用し、最大幅29mm、全長58mmで、球体から缺球を取り除いた後に円錐を組み合わせたような2:1の比率をもちます。下部に直径0.7mm全長120mmのピアノ線にナツメ型中通しオモリ5号を装着しています。浮揚時に頭部が僅かだけ露出するように計算したことで寸法がかなり半端な印象を受けます。実験では全く同体積、同表面積の験体を2体製作しました。両験体の誤差は浮揚した状態で0.5%以下です。 浮揚した状態を基準としたのには、それなりの理由があります。バルサ材には、木の目が存在します。この為に硬く重い部分と、柔らかく軽い部分とができます。可能な限り均一なものを探して製作してはいますが、完璧に同じ状態のものはありません。故に同体積、同表面積でも、微妙に重量が異なります。アルキメデスの原理からもお解かり頂けるかと思いますが、両験体を同じ条件下で検証するには、オモリを削り浮力を微調整する以外方法がありません。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
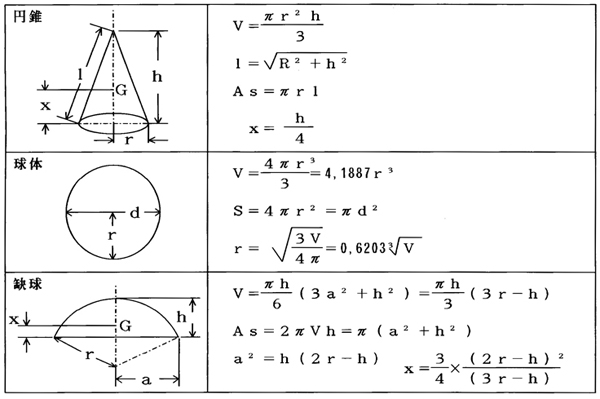 【図-46】 験体の製作に関する各立方体の容積および諸数値 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 実際に験体を製作するには幅が35~40mmで厚さが20mm程のバルサ材を使用します。バルサは硬い部分と柔らかい部分との落差が激しく、綺麗に成型するには、刃先が鋭いカッターナイフが適しています。通常験体一つを仕上げるのに何枚かの刃を必要とします。刃先が鈍った状態で使い続けるとバルサが木目の所でめくれてしまいます。 最初の作業は目的とする験体の寸法を製図し、型紙を作ります。この型紙をバルサにあてがい、周囲を余裕をもってカットします。この切り出したバルサ材が2枚で1体の験体になる訳です。 次に、この2枚のバルサの間に下部オモリを装着するピアノ線を挟み込み、瞬間接着剤を塗布し充分に圧力を加えて密着、固定します。この圧着過程がいいかげんだと、隙間ができ後々の作業に支障をきたします。 圧着が完了したものは、ノギスで採寸しながら成型してゆきます。成型はカッターナイフで大雑把に削り取ってゆきますが、削り過ぎには充分注意しなければ元も子もなくなります。桐素材と異なりバルサは脆く、加工が簡単なようで難しい面があります。ある程度切り出したら、験体をピアノ線を軸に回転させながら、ブレをサンドペーパーで修正してゆきます。塗装段階を除き、慣れれば1体を1時程度で仕上げられるようになります。 上の【図-46】は円錐験体を製作するのに必要な諸数値です。ご自分で同じ験体を製作して再確認してみたい方は参考にして下さい。 実際のウキの体積と表面積の計算は、大変複雑で微分や積分の計算も必要とするので面倒です。製作した験体では贅肉をそぎ落としているので、その分面倒な計算が減ります。また験体は直線で構成される面が出現しますが、運動に及ぼす影響は特に無いとお考え下さい。 尚、上の表の缼体の半径rでは、現実の計算では缼球の半径1aに相当しません。故に単純に球体から缼球を引き、それに缼体を加えても験体のVとSは求められません。これを求めるには【図-47】の式が必要です。表面積Sでのnは、球体に対しての倍率です。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
【図-47】 験体のVとSを求める数式 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 微調整を施された験体はいよいよ本格的に運動能力の比較実験へと進みます。水槽実験は球体の験体の場合と同様に、水温12℃±1.0℃で行ないます。【図-48・49】を見ればご理解頂けると思いますが、水は10℃でその重量が997.7有り、15℃でのそれは101.88となります。 即ち、2体の験体の浮力の差が極めて小さい時、片方が10℃で浮揚していても、15℃では沈下することも有り得る訳ですので、更なる微調整を施すには、飽和食塩水を使います。浮揚させての微調整でも充分な精度が出ていると言えますが、水の比重を高め、より高い精度を目指します。最初に浮揚させて微調整した2体の験体を、小さいオモリを装着し沈下、着底させます。次に少しずつ飽和食塩水を注ぎ、よく混ぜてゆくと、ある時点で着底した験体が片方だけ浮揚します。これでどちらの験体が浮力が大きいかの判断がつきます。あまり意味のあることとは思いませんが、これぞと思う験体には双方ともこの作業を施しました。自己満足ですが、この過程での浮力の誤差は0.1%を完全に切る筈です。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
【図-48】 水の重量と密度 【図-49】 純粋な水の比重 重量 r=1000kg/m3 (1atm 4℃) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
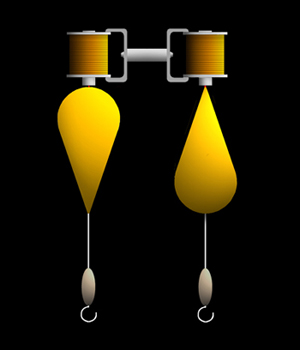 【図-50】 電磁石を使った験体落下装置 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 球体の実験と同様に、流体中で験体が示す抵抗を観察する目的で行ないます。何度も記すようですが余り好きな実験ではありません。しかし、形状に由来する後部渦流の及ぼす影響を探るには止むを得ないと考えます。 この実験では球体の連続負荷実験で使用した0.5~5.0号までの丸型と、B・2B・3B のガン玉の計10種類のオモリを用意しました。この実験では市販のオモリそのまま使用しますので、それぞれオモリを取替えて同じ実験を2度行ないます。 方法は、球体の時と基本的には変りませんが、こちらは2体同時に観察する必要があります。当初は電磁石を利用した打撃装置同様に、験体頂点に打ち込んだ鉄製ビスを電磁石に吸い付かせて落下させる方法を採用しました。しかしかなり強力な磁力が必要(電力も…)なのと、やはりビリビリ。結局、最終的に採用したのは両手で1体ずつ摘んで離すと言う、簡単にして、原始的で、確実な方法です。 ●連続負荷実験の結果(沈降実験):負荷したオモリの大小に拘わらず、全てシズク型が大幅にドングリ型を凌駕しました。これは阿波ウキのドングリ型がシズク型より抵抗が少ないと言う、一般の評価と明らかに異なる結果です。また、実験では、沈降時の初速も平均速度もシズク型がドングリ型を遥かに上回りました。【図51・52】はその結果です。両験体の落下2秒後の到達深度の差を記録したデータが有ったのですが、残念ながら見当たりませんでした。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
● 優 ● 劣
【図-51】 着底までの所掌時間 【図-52】 単一時間内の到達深度 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ●連続負荷実験の結果(浮揚実験):【図-53・54】にあるように、予想した通りの完全に間逆の結果がでました。浮揚性能ではドングリ型がシズク型を大幅に凌駕したのです。浮力に大きな差がない場合は、ゆっくりとドングリ型が先行しますが、浮力の増大に従って速度が急激に上昇します。この下線の部分はウキの形状を決める際に、大変に重要になってきます。一見ドングリ型が優れているかのような印象を与えますが、あくまでもデータ上のことで、実際のウキに適用するには大きな問題を孕んでいます。(このことに関しては徐々に説明してゆきます) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
● 優 ● 劣
図-53】 浮揚までの所掌時間 【図-54】 単一時間内の浮上深度 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| これらのことから重要な事柄が見えてきます。即ち、運動方向に対してはシズク型がドングリ型より抵抗が少ない形状であるとの証明と同時に、丸い後部は発生する渦流の影響を受け易い形状であると言う事実です。これらの事柄はウキの性能を左右する要件です。
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| この実験は波浪中でドングリ型とシズク型の2体の験体が示す安定性と視認性とを、水道圧で故意に作り出した乱流を使って検証します、 ウキの世界は、実験でもしなければ正確には解らない事柄に満ちています。その中にあって視認性は目で優劣が判断できる数少ない部分です。また安定性も「安定性とは何か」をしっかりと理解していれば、目で確認し判断できる要素が多く有ります 実験では、験体の浮力を限界ギリギリまで落とし、両験体ともほんの僅かだけ頂点を露出するよう調整してあります。球体同様に実験中の験体は殆どのあいだ水面下にあります。まずこのことを頭に入れてデータを読まなければなりません。単にデータ上の優劣のみで安易に判断すると、連続負荷実験(浮揚実験)の結果同様で真の意味を誤解してしまう危険性があります。そして理想的なウキの形状は永遠に求められなくなります。データを読むことは得られた結果を読み解くことにあります。 ●安定性と視認性の実験:乱流中ではシズク型験体は、渦に飲み込まれるかのように僅かにその頭部を水面下に埋没させます。ドングリ型験体は、渦に巻き込まれることなく、常に水面付近を浮揚しています。水面下へ沈下しないだけ視認性はシズク型験体より優れているように見えます。しかし、乱流の発生していない時の水面位置(赤線)から比べると、シズク型験体は沈降方向への動きが大きく、ドングリ型験体はその逆方向への動きが多いことが判ります。【図-55】 この実験を視認性の面だけで捕らえると、ドングリ型がシズク型を上回っているかのようです。注意しなければならない点は、波浪中でどれだけ水面から離れるかが重要です。 シズク型験体は、浮上能力がドングリ型験体より劣るため、波から受けたエネルギーを沈降方向へ相殺しようとし、それに伴い浮上が一瞬おくれます。ドングリ型験体は、沈下能力がシズク型験体より劣るため、沈降方向でのエネルギーを相殺できずにプカプカと跳ねるように、絶え間なく水面上にその頭部を現します。 つまり、ドングリ型験体の視認性の高さは、その形状が優れていることに由来するのではなく、単に運動能力の低さに由来します。世間に視認性が高いと誤って伝わってしまったことが検証できます。 波浪中での安定性は、上下動が激しいドングリ型験体に比べ、シズク型験体は上下動が少なく安定しています。また水面付近の横からの流れの影響もシズク型験体が少なく、ドングリ型験体の揺れがより大きくなります。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
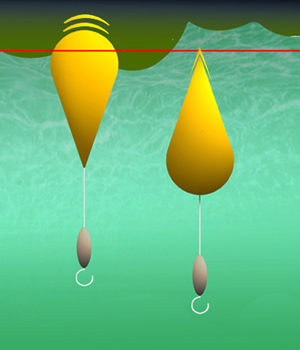 【図-55】 視認性の実験 赤線は水面の高さ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Traditional Japanese colors |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
